How To Compare Treasury Bill Rates to Bank Account APY

With T-Bill rates now around 2%, here’s another topic that is getting some interest for the first time in many years. Individual investors can buy short-term Treasury Bills (4, 13, 26, and 52 weeks) via non-competitive bid at either TreasuryDirect.gov or from a brokerage account with a bond desk. (I’ve used Fidelity and Vanguard in the past.) You can find Treasury Bill rates at several places, but here are the official sources:

• Treasury Direct (auction results)
• US Treasury website (daily market rates).

An individual investor might ask – How do I compare Treasury Bill rates to Savings Account interest rates? Here is a step-by-step walkthrough to convert from the weekly auction results to a bank’s quoted APY interest rate.

Find the investment rate (not discount rate) from the recent auction results page. This is the equivalent of Annual Percentage Rate (APR). It is based on a 365-day year and reflects the annualized rate to maturity. Here’s the most recent snapshot from 9/13/2018:

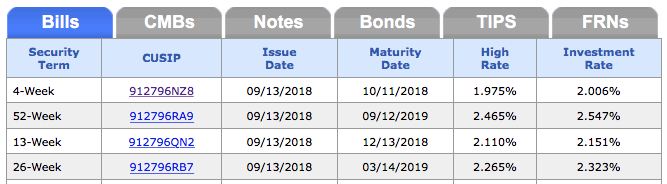
Let’s take the 4-week (28-day) T-Bill, which has an APR of 2.006%, or 0.02006.

Convert this rate to APY. Annual Percentage Yield (APY), as opposed to APR, takes into account the effect of compounding interest. It’s also a higher number, which is why most banks just tell you the APY. An approximate way to convert it to APY is using this formula:

APY = (1 + (APR/PeriodsInAYear) )^(PeriodsInAYear) - 1

For our case, the APR is 0.02006 and PeriodsInAYear = 365/28. You could just copy and paste this formula into a Google box:

(1 + (0.02006/(365/28)))^(365/28) - 1

The resulting number is 0.2024, or 2.02% APY. Since rates are still relatively low, the difference between APR and APY will be small over a year.

Note that you can’t actually reinvest all of the money from a maturing T-Bill directly into a new T-Bill. For example, you might get back $1,000 from your first T-Bill, but can only reinvest $995 of it in the next T-Bill. The rest must sit in a savings account (with a competitive interest rate hopefully).

If you don’t pay state or local income taxes, you can stop here. As you can see, it’s very competitive with high-yield savings accounts.

Adjust for state and local taxes to find Your Tax-Equivalent Rate. Treasury Bills are exempt from state and local taxes. If you have to pay state and/or local taxes on bank interest, then this may put T-Bills ahead by a bit more. You can use my tax-equivalent yield calculator for this purpose. You’ll need to know your marginal tax rates and whether you can deduct your state taxes paid on your federal tax return.

Let’s say you are in the 22% bracket federally, 9% for state, and will itemize. For that situation, this specific 4-week T-Bill will earn the same amount of interest (after taxes) as a bank account earning 2.28% APY. You can do the same thing to the 3-month, 6-month, and 1-year T-Bills (13 week, 26 week and 52 week, technically). You may (or may not) find this final number to be more attractive than a bank account.

Also see: How To Build A 4-Week Treasury Bill Ladder: A Visual Guide