Fidelity has a new tool called the myPlan retirement calculator. It’s very soothing and is only 5 questions long, why not give it a whirl? What I like about it is that it doesn’t just deal with average numbers. People like to use round numbers like 8% annually and pretend like they are a sure thing, but the fact is with some bad timing we could end up doing a lot worse.
Using some rough numbers from our own situation – age 28, $100k income, $100k saved so far, $2,500 saved monthly, Aggressive Growth investment style, we get the following result:
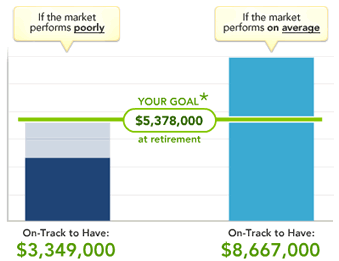
Not bad, right? If the market performs on average, we will easily exceed what we need to retire on. (Yes, the numbers are huge!) If the market performs poorly however, we’ll be significantly short. Now, what if we change the investment style from Aggressive to Conservative?
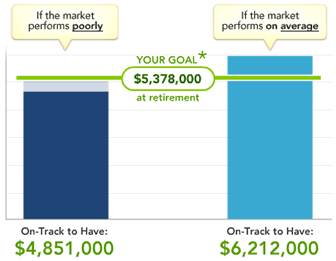
As you can see above, this improves my Poorly scenario significantly, while worsening my Average scenario. But overall, I am virtually assured of being very close to my goal amount regardless of luck. This poses an interesting question: Should those that are saving significant amounts of money towards retirement choose a less aggressive portfolio in order to better guarantee reaching their savings goal? Or should they just play off the averages?
I suppose in theory if someone saved enough they could simply invest entirely in inflation-protected bonds that guarantee a real return. I’m also confused as to whether the calculator is crudely assuming that I would keep the same asset allocation for the entire period from age 28 to 65. Your thoughts on this and the calculator overall?
The Best Credit Card Bonus Offers – October 2024
Big List of Free Stocks from Brokerage Apps
Best Interest Rates on Cash - October 2024
Free Credit Scores x 3 + Free Credit Monitoring
Best No Fee 0% APR Balance Transfer Offers
Little-Known Cellular Data Plans That Can Save Big Money
How To Haggle Your Cable or Direct TV Bill
Big List of Free Consumer Data Reports (Credit, Rent, Work)
Looks like your set, I’m just trying to save 1 million
I couldn’t find in their methodology about how they determine your contributions thereafter. Do they look at your present contribution to income ratio and then maintain that while building in salary growth (as stated in their assumptions)?
The calculator looks nice. I’m impressed.
How did you come up w/ your $2,500 a month figure? Is that what you can truly save now, or an estimated average what you can save every month until age 65? Those are generous and exciting figures. A good motivator to save money…
The fact that you can make adjustments and see changes reminds me of a watered down version of Morningstar’s (where you can see what happens when you change specific investments). It is refreshing to see the unknowability of the market reflected in some way, that is something I have never seen.
It is obvious that your results will depend somewhat on how well the market does, but it is so much more believable in that graph. This is much better than most calculators I have seen. The best one I have ever seen is in Morningstar, but that is not free, except for your free 14 day trial.
I read Fidelity’s “assumptions and methodology” and it seems like they apply the same model portfolio throughout the entire scenario. It is probably more realistic to build a model using different levels of risk as the investor approaches retirement.
In other words… I think that both the downside and upside are overstated. When you’re 55 you will be less aggressive and therefore you should have less downside risk but also less upside potential.
You know, I was just thinking about this in relation to what my parents have done. They are major savers, but not aggressive at all. From the start they saved a significant portion of their income and invested mostly in safe products (CDs & Bonds). Now they are set and have no worries. While they could have done better being heavy in stocks through the boom of the 90’s, their saving stategy still paid huge dividends.
The funny thing is that anyone trying the same thing now would be told that there is no way they could beat inflation. I wonder if they heard the same things when they were younger.
Jonathon,
When is the retirement horizon for your MyPlan estimates? Are you assuming both you and your wife working full-time and no added expenses (i.e. children) during this time? A child will certainly reset your yearly allocations and then you have the 529 monster to balance with the retirement funds.
My wife and I faced this decision this year and realized that (according to a variety of the college cost calculators, lump sum funding of the 529 is a tremendous advantage over dollar-cost averaging so we’re taking a chunk of our taxable investments (401K and others at max already) and funding a 529K for our three month year old.
The important thing was planning to have a sizable liquid cash fund available for this new investment. We used laddered T-bills and progressively added to the rollovers then when we were parents made the shift. Planning for retirement also requires planning other life events.
I think
heres what i dont understand about everyone’s mentality.
if you are able to save $1,000,000, which YOU should be able to do within the next decade. You can invest that money into assets that are going to throw off cash flow. You can get 5% tax free municipal bonds and be living off of a $50,000 income without even touching your principle.
thats just one consideration. why not invest in some income property. you could have another $50k in cash flow some day + appreciation.
there is no need to touch the million
Jonathan – By going a less aggressive route, you will surely reach your goal. But, you have to keep in mind your current goal is subject to change.
You have the opportunity to be somewhat more aggressive now and chase larger returns. As you get nearer to retirement your wants and needs will change. You are very fiscally responsible, so I don’t see you entering into retirement with a huge sum of debt. That will be your key. Hopefully, your biggest retirement questions (as well as the rest of us!) should be: Should I buy a vacation home/travel; how much should I pass on to my heirs? As you get closer to retirement, you can change your investment style to suit your needs/goals. For now you should be in a well-directed, accumulation mode and reallocate as your needs/goals change.
Marshall Middle – there is nothing wrong with shooting for 1 million. Everyone needs a goal and everyone has different needs. Your goal of 1 million may be enough for you – especially when you consider what your situation will be when you retire. My grandparents are retired and living on a small fixed income. They only have around $100,000, mostly in CDs and similar investments. But they own their house, and have no debt. They have enough flexibility to travel every so often and do everything they want. The key is they have no debt and live within their means.
This is cool…
OK, here’s the thing that bugs me about this calculator. Given your figures, you currently save 30K/year on a 100K/year salary, so you are living on 70% of your salary, give or take some taxes. But the calculator assumes you to live on 85% of your salary at retirement, by which time you will be no longer saving, yes? So basically they want you to have enough money to live better in retirement than now?? That doesn’t make sense to me. I’m leaning towards spending big money on http://www.esplanner.com/ ($150-200) when I want to determine how much money I’m going to try and save up. If they had made it for mac, I’d have bought it already.
I find it hard to believe that you can save $100k/year when you only make $100k/year..
Marhsall When are you retiring? If you are retiring in 30 years, $1 million might not be enough due to inflation. If you are retiring next year it might be fine.
How do you save $2500 mo? I have same income, but I am a homeowner. I am lucky to save $750 month. what is your rent again? Have you calculated how buying a home will effect your savings rate considering there are a number of additional expenses that come with ownership.
According to my calculations, that 3.349 million estimate is assuming a rate of return of only about 5%. Even if the market performs poorly, I think your returns will beat 5% on average.
this is cool did anybody contact fidelity?
nice find.
where are all these people finding jobs that pay $100,000? Must be nice!
Joe, let me ask you a question. You say you make roughly the same income — about $100K. Well surely you haven’t been making that much the moment you started working right? So if you were able to live on X back then, what’s stopping you from living on X+inflation now? Now deduce X+inflation against your current salary and there you have the answer — it’s not how much you make but how much you spend.
Now before you start saying “but marriage, but kids, but house…”, I am married with a kid so I know firsthand what costs are mandatory and what are discretionary. If you don’t give a crap about mcmansions or consumer possessions, it’s not a big deal to save $2500/mo or more. My salary combined with my wife’s is not much more than you make alone and we’re easily in the “more” category.
What you going to do with that money? Who needs 4mil then tehy are 65.. 😀 Those people play cards – that is it..
I think it’s better to spend money now ir live life!
“100k saved” should be “100k saved thus far”, as in the 3rd myPlan question.
The numbers I threw out there are just examples and will be off in the future, whether it’s the income going up, or the savings going down, or whatever.
I was mainly commenting that sometimes the downside is lost when thinking about the upside, and that Fidelity is actually pointing that out. Notice there is no column for performing “well above average”.
Whenever you read about older people who haven’t saved as much, the solution is often “Oh! You need a higher % in stocks to boost your return so you can catch up to your goals!” I always cringe at that idea. By that logic, if you really haven’t saved enough why not just play Roulette and bet on black a few times?
Those numbers aren’t adjusted for inflation. They are still hefty, but also bigger by a least a factor of 3 due to inflation.
This is neat. I’m on track to have $4 million for retirement if I continue with my current annual salary of $25,000 (saving about half), which presumably will go up once I stop being a student.
I see the same thing (we’re a bit older, but saving a good bit more). When we’re aggressive, we can shoot the moon with average perforamce, but significantly underperform our goal with poor returns. Scaling back helps us out considerably on the downside, to the point that we’re exceeding the goal amount if we’re conservative. Of course, the upside is then greatly reduced. Interesting.
I have been a Fidelity Customer for more than 11 years and they have one of the best brokerage services IMO. This tool is pretty but i would like to know the formula behind this, Stocks: 10% gain on Average where bonds leads 6-7%?